ハローワークで職業訓練(教育訓練)を申し込もうと考えている方で、「試験があるって聞いたけど、どんな問題が出るんだろう?」「難しくてわたしには無理かな?」と悩んでいる方はいませんか?
実際に職業訓練校の方にお話しを聞いてみたところ、中学校卒業~高校1年生(が少し)程度の難易度で全国的に出題されているそうです。
ハローワークを経由した職業訓練校は、受講開始時に失業保険の給付日数が残っていれば(注:他に細かい給付条件あり!)最長2年間受講期間中、毎月10万円の給付金をもらいながら学べるということから年々人気が高まっており、受験倍率も増加しています。
ずっとやりたかった事を、年齢や環境で諦めてきたひと。
収入がなくなることが怖くて、前向きな一歩を踏み出せずにいるひと。
じぶんを変えたいけれど、どうすれば良いかわからずもがいているひと。
それぞれの厚生労働省のホームページやハローワークのホームページで、受けることのできる職業訓練を一覧形式で確認することができます。
都道府県ごとに受けることができる職業訓練や受講期間が違い、住んでいる都道府県を越えて受講することもできるので、やってみたいこと・興味のあることを探してみることから始めてみませんか?
実際に出題された過去問と答えをつくりましたので、参考にしてぜひ合格をつかみ取ってください。
※問題の右側にある【▼】をクリックすると答えが表示されます。

問1 次の各問いに答えなさい。
⑴ 次の計算をしなさい。
① ー3ー(ー8)
5
② 6✕(ー7)
−42
③ $4\times(5^2-12)$
52
④ 0.6ー0.83
−0.23
⑤ 32÷0.4
80
⑥ $\frac{3}{7}\div\frac{2}{5}$
$\frac{15}{14}$
⑦ $-\frac{5}{14}+\frac{8}{21}\div\frac{2}{3}$
$\frac{3}{14}$
⑧ $(-6)^2-5^2$
11
⑨ $\sqrt{108}-\sqrt{48}$
$2\sqrt{3}$
⑩ $-2(3x-4y)+3(5x-7y)$
$9x-13y$
⑪ $30a^4b^5\times(-7a^2b)\div21a^2b^3$
$-10a^4b^3$
⑫ $\frac{x+1}{5}+\frac{2x-1}{3}$
$\frac{13x-2}{15}$

⑵ 0° ≦ θ ≦ 90°のとき、次の等式を満たすθを求めなさい。
$sinθ=\frac{\sqrt{3}}{2}$
θ = 60°
⑶ 次の3つの数から最も大きい数を答えなさい。
$\frac{\sqrt{5}}{4} , \frac{4}{7} , 0.54$
$\frac{4}{7}$
⑷ $xについての1次方程式 3x-4a=2x+2a の解が x=3 のとき、aの値を求めなさい。$
$a=\frac{1}{2}または0.5$
⑸ 次の2次方程式を解きなさい。
① $x^2-9x=-20$
$x= 4 , 5$
② $3x^2-12x=-231$
$x= -7 , 11$
⑹ 次の連立方程式を解きなさい。
・$2x+5y=9$
・$3x+4y=3$
$x = -3 , y = 3$
⑺ 次の式を展開しなさい。
$(2a-3b)^2$
$4a^2-12ab+9b^2$
⑻ 次の式を因数分解しなさい。
$3x^2-4x-7$
$(x+1)(3x-7)$
問2 次の各問いに答えなさい。
⑴ ある商店で、4月1日に1個2,000円で売った商品を4月2日に1個1,800円で売ったら、売り上げ個数は4個増え、売り上げ金額は5,000円増えた。
4月1日の売り上げ個数を求めなさい。
11個
⑵ 大小2つの整数がある。2つの整数の和は −14で、2つの整数の積は −72である。
このとき、小さい方の整数を求めなさい。
−18

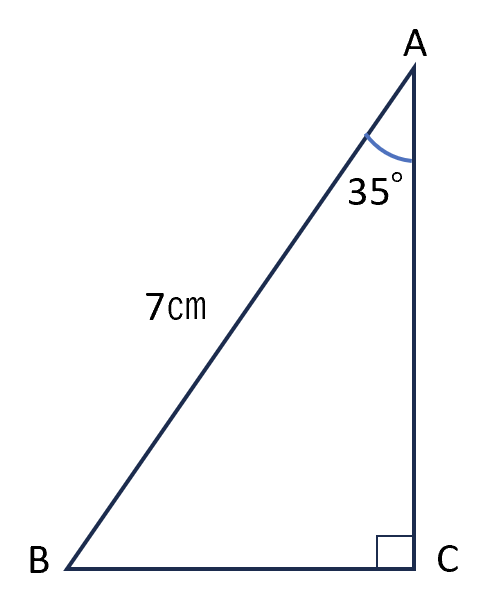
⑶ 下の図において、AB=7cm、∠BAC=35°のとき、ACの長さを求めなさい。
ただし、$sin35°=0.574、cos35°=0.819$とする。
5.733cm
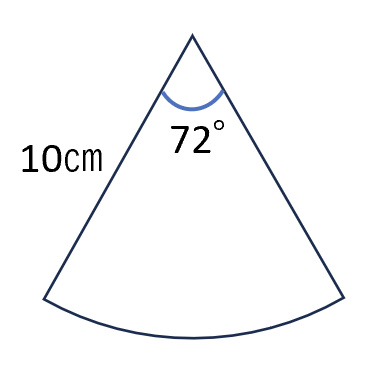
⑷ 下の図のような、半径12cm、中心核72°のおうぎ形の面積を求めなさい。
ただし、円周率をπとする。
$\frac{144}{5}π ㎠(または 28.8π ㎠)$
⑸ 長さ56cmの線分を2つに分けて、それぞれの線分を周の長さとする正方形を1つずつ作り、2つの正方形の面積の和を100㎠としたい。
このとき、大きい正方形の1辺の長さを求めなさい。
8cm
問3
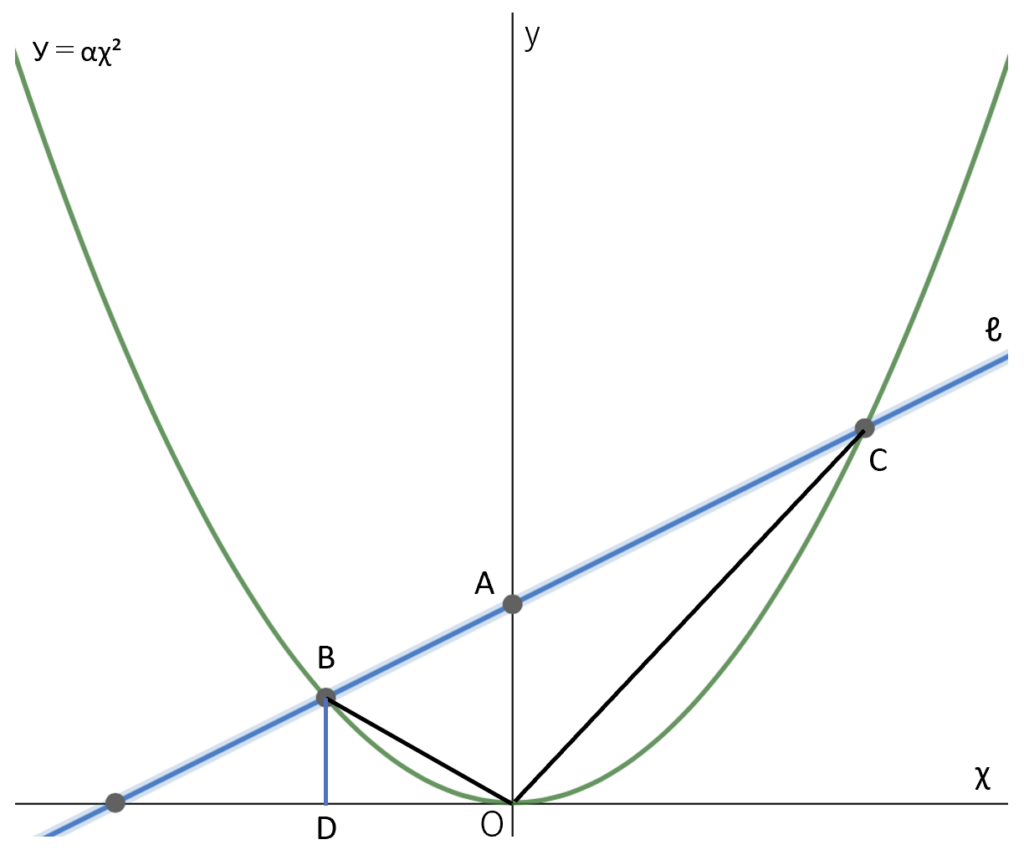
下の図のように直線 $y=\frac{1}{2}x+2とy$軸の交点を A 、直線 $y=\frac{1}{2}x+2と放物線 y=ax^2(aは定数)$の交点を B、C とし、点B から$x$軸に引いた垂線を BDとする。
台形 ODBA の面積が3㎠のとき、次の各問いに答えなさい。
⑴ 点 B の座標を求めなさい。
(−2,1)
⑵ $a$の値を求めなさい。
$a=\frac{1}{4}(または0.25)$

⑶ 点 C の座標を求めなさい。
(4,4)
⑷ △OBCの面積を求めなさい。
6㎠
⑸ 直線 CD の方程式を求めなさい。
$y=\frac{2}{3}x+\frac{4}{3}$
※災害避難で持っててよかった!・・防災士が【厳選】これだけ備えて5選


